Highest damaging hit attainable

lelag200

I finished a fighter/thief solo the other day and was proud to see damage output around 100 on back-stab crits with staff +3. However, I got thinking about how much more damage could a thief do with x4 backstab despite proficiency limits with weapon and style. Really I'm looking into killing Sarevok with one critical because that would be fantastic to see.

To my knowledge, the following setup is as good as it gets when trying to reach the highest damaging hit attainable (without cheats)---> Level 10 Theif or Assassin backstabbing with Staff of Striking wearing Gauntlets of Expertise, buffed with a potion of cloud giant strength and Draw Upon Holy Might to bring strength to 25.

If research is right then I should be able to kill Sarevok in one blow as his physical resistance is only 10% at hp=135. Am I missing anything that could improve on damage output?

lelag200

If you can't see that text, that hit was 180 damage.

Ulsh

Haven’t thought about it myself, but someone else has:
https://lilura1.blogspot.com/2020/01/Baldurs-Gate-Maximum-Backstab-Damage-Biggest-Backstab.html

OlvynChuru

lelag200 wrote: »

If research is right then I should be able to kill Sarevok in one blow as his physical resistance is only 10% at hp=135. Am I missing anything that could improve on damage output?

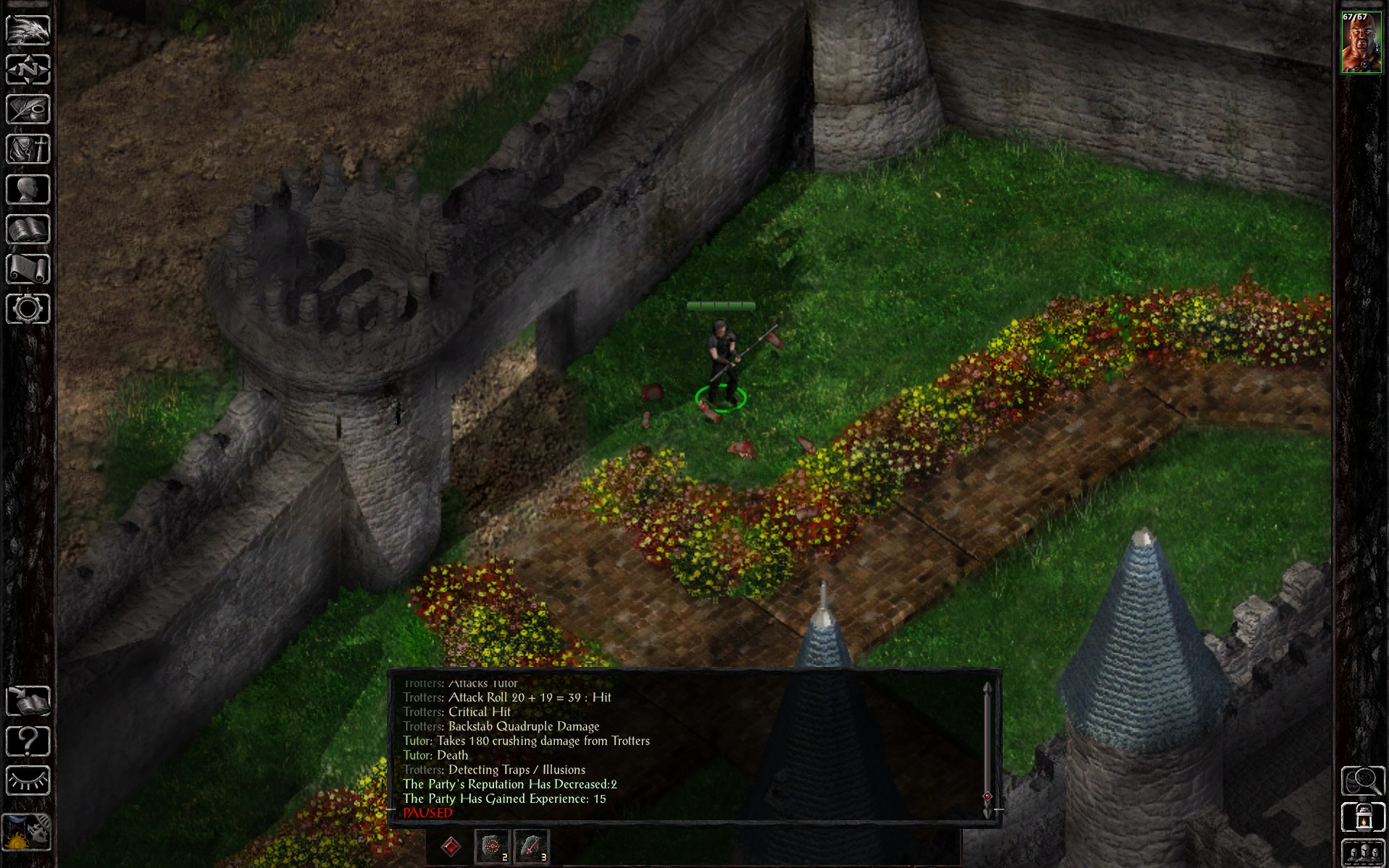
Keep in mind that the tutor is unarmed, which gives you +4 damage against them, so that critical backstab would've done 32 less damage had the tutor been armed like Sarevok.

Also, Sarevok wears a helmet in the final battle, so you won't be able to critically hit him anyway.

If you're just looking to see how much damage you can do to an unarmed creature, you could deal even more by having other party members buff the character. A cleric can cast Bless and Aid on them, and a skald could sing their bard song. Those three things would give the character another +4 damage, or +32 after multipliers.

lelag200

I didn't know about the unarmed dmg bonus. The fact that that bonus exists at all seems odd. It is also new to me that Sarevok has the only functional helmet in the game aside from PCs. After testing, I could only do 90 damage tops to Sarevok (with an additional +4 poison) with the assassin.

Taking all into consideration it seems like 126 (according to the wiki you get +1dmg from bless +1 from aid and +4 from bard song which means 6x4=24. 102+24 = 126) is the hard limit on damage possible to Sarevok in 1 hit. Then again, I may not understand how the outside character bonuses play into the formula on that link Ulsh shared.

jmerry

More damage: Mage-Thief 9 dual class, using Polymorph Self ogre form. You won't have enough mage levels to cast from spell slots, but Sorcerous Sundries has 20 copies of the scroll. 4d6+1 weapon damage, 4x backstab. Strength 20 (18/00 form, +2 from Bhaalspawn DUHM). It's a one-handed weapon with no proficiency, so weapon styles and proficiencies won't add to the damage - though single-handed style doubles your critical chance.
Additional damage before backstab multiplier: +2 from gauntlets, +1 from Bless, +1 from Aid, +2 from Skald song.

A maximally vulnerable target (no helmet, no melee weapon), then, takes ((4d6+1+6+4)*4+9)*2 damage in a critical backstab, for up to 298 damage. A target with a helmet and a melee weapon takes (4d6+1+6)*4+9 damage, for up to 133 damage.

So ... I'm pretty sure you can't kill Sarevok in one hit (effectively 134 HP). Or the Demon Knight (125 HP, 10% resistance). Aec'Letec is a yes (106 HP, no resistance or crit protection), though the usual caveats for that fight apply.

... wait, I forgot about the violet potion. That can get you a bigger strength value. Apply it after turning into an ogre.

With that tweak, the strength bonus increases from +9 to +14, and the best backstab against a protected target is 138 HP. With a perfect damage roll or one less, you can kill Sarevok in one hit - or rather, drop him to 1 HP so his script kicks in and ends it. Sarevok has a non-removable min-HP item.

Now, the odds of that damage roll ... 5 in 1296. Ouch. You're going to need a lot of luck. A Bard, a Blade, and a Luck spell can get you +3 luck, so a natural 3 or better becomes a 6. Odds increased to 32/81, slightly less than 40%.

Grond0

jmerry wrote: »

More damage: Mage-Thief 9 dual class, using Polymorph Self ogre form. You won't have enough mage levels to cast from spell slots, but Sorcerous Sundries has 20 copies of the scroll. 4d6+1 weapon damage, 4x backstab. Strength 20 (18/00 form, +2 from Bhaalspawn DUHM). It's a one-handed weapon with no proficiency, so weapon styles and proficiencies won't add to the damage - though single-handed style doubles your critical chance.
Additional damage before backstab multiplier: +2 from gauntlets, +1 from Bless, +1 from Aid, +2 from Skald song.

A maximally vulnerable target (no helmet, no melee weapon), then, takes ((4d6+1+6+4)*4+9)*2 damage in a critical backstab, for up to 298 damage. A target with a helmet and a melee weapon takes (4d6+1+6)*4+9 damage, for up to 133 damage.

So ... I'm pretty sure you can't kill Sarevok in one hit (effectively 134 HP). Or the Demon Knight (125 HP, 10% resistance). Aec'Letec is a yes (106 HP, no resistance or crit protection), though the usual caveats for that fight apply.

... wait, I forgot about the violet potion. That can get you a bigger strength value. Apply it after turning into an ogre.

With that tweak, the strength bonus increases from +9 to +14, and the best backstab against a protected target is 138 HP. With a perfect damage roll or one less, you can kill Sarevok in one hit - or rather, drop him to 1 HP so his script kicks in and ends it. Sarevok has a non-removable min-HP item.

Now, the odds of that damage roll ... 5 in 1296. Ouch. You're going to need a lot of luck. A Bard, a Blade, and a Luck spell can get you +3 luck, so a natural 3 or better becomes a 6. Odds increased to 32/81, slightly less than 40%.

You can actually do it more easily than that. In the damage section you've assumed the effects only from the Skald song, but adding the impact of the Bard and Blade songs gives a further 2 to the base damage, making the total achievable 146. You can also have a Chant spell active. That doesn't increase the maximum damage, but does make it more likely you will get that damage (acting as a luck bonus). With that and the 3 bard songs active the chance of a one-shot kill becomes a near-certainty (1295 out of 1296 if I've got my sums right ).

Grond0

lelag200 wrote: »

I didn't know about the unarmed dmg bonus. The fact that that bonus exists at all seems odd. It is also new to me that Sarevok has the only functional helmet in the game aside from PCs. After testing, I could only do 90 damage tops to Sarevok (with an additional +4 poison) with the assassin.

There are loads of enemies with such helmets - think of hobgoblins or half-ogres for instance.

jmerry

Grond0 wrote: »

In the damage section you've assumed the effects only from the Skald song, but adding the impact of the Bard and Blade songs gives a further 2 to the base damage, making the total achievable 146.

Not how luck works. Luck increases the chances of high damage rolls but doesn't increase the maximum possible. The non-skald bard songs are there to boost our chances of getting the rolls we need, not to boost the base damage.

Grond0 wrote: »

You can also have a Chant spell active. That doesn't increase the maximum damage, but does make it more likely you will get that damage (acting as a luck bonus). With that and the 3 bard songs active the chance of a one-shot kill becomes a near-certainty (1295 out of 1296 if I've got my sums right ).

This, on the other hand ... if Chant actually functions as luck (they're different opcodes), then that's a big boost. We only fail if it's a natural 1 on two or more of those four dice. 1/1296 for four 1s, 20/1296 for three 1s, 150/1296 for two 1s, 500/1296 for one 1, 625/1296 for no 1s. That gets us up to 1125/1296, or 86.8%.

Incidentally, the description of Aid says "the benefits of a Bless spell (+1 to attack rolls and saving throws)". Does it actually boost damage, or not? If it doesn't, then our maximum damage is 134 and we need perfect rolls

As for hitting Sarevok ... AC -5, no modifier against crushing. This character has base THAC0 16 from thief levels, no to-hit bonus from the weapon, +1 from gauntlets, +2 from skald song, +1 from Bless, +1 from Aid, +1 from Chant, +4 from invisibility, and +7 from strength. I'm not sure if luck works on to-hit rolls, but a potion of power would boost that to the point of hitting on a 2 even if it doesn't. Only rendering Sarevok helpless would make it more certain.

And ... another way to do better. We already have a cleric in the mix to cast buffs. Make that a priest of Tempus (such as Branwen), and use Chaos of Battle. One of the possibilities (a 10% chance) is a luck bonus, +2 at priest level 7. If that comes up, it's as good as the bard and blade songs combined. Stack it with the rest for an absolutely certain maximum damage roll, or just replace those two characters so we're only using half the party on this insane scheme.
As for that 10% chance ... the effect is locked in for the full 1-turn duration as soon as you cast it. You can rest out in the Undercity repeatedly until you get the right version, and then go in for the kill.

Grond0

jmerry wrote: »

Grond0 wrote: »

In the damage section you've assumed the effects only from the Skald song, but adding the impact of the Bard and Blade songs gives a further 2 to the base damage, making the total achievable 146.

Not how luck works. Luck increases the chances of high damage rolls but doesn't increase the maximum possible. The non-skald bard songs are there to boost our chances of getting the rolls we need, not to boost the base damage.

I must still be half asleep - talking about the impact of luck in one half of a post and ignoring the same effect in the other .

lelag200

This is great input, thanks all! I have to try this out now. I will get back with a screenshot when successful.

lelag200

It worked! jmerry's "insane scheme" took Sarevok down in one blow. Unfortunately, the cutscene came on before I could pause to see what the roll was/get a screenshot. I'll have to replicate this later to get one.

sarevok57

hokay, i did some testing, and it looks like the maximum amount of backstab damage you can do is 138

i did the mage 1 dual thief 9 combo

transformed into ogre

had 25 STR

mits of weapon specialization

bless
aid
chant
tempus chaos
bard song
skald song
luck spell

and this is what it looks like;



and after many, many, MANY reloads, there seems to be 6 different damages you will deal, im guessing its just a straight up 16.666% chance on which one you deal, because these were the only 6 i saw;

118, 122, 126, 130, 134 and 138;



i never saw the damage go pass 138 ( except for the crit that did 276 )

so if you were to use this backstab combo on sarevok, it would have a 33.333% chance of taking him out in one hit

since he has 135 HP but his item is scripted that once he hits 1 HP or less to do its thing, so you only need to deal 134 damage to him

jmerry

No, we did (at least some of) the math earlier in the thread. They aren't equally likely outcomes.

If you have all the luck - meaning that you got the right version of Chaos of Battle, at cleric level 7 or higher - then it's absolutely guaranteed to give you the maximum 138 damage. Only a (critical) miss on the attack roll can stop you.

With +3 luck (no CoB), it's about 1/5 each to get 134 or 138 damage, and could theoretically go as low as 106. But that's down in the extremely unlikely tail. Your six observed outcomes cover about 98% of the possible outcomes. Probabilities, assuming a random version of CoB:

138: 27.8%
134: 17.8%
130: 24.4%
126: 14.1%
122: 10.1%
118: 3.6%
114: 1.5%
110: 0.3%
106: 0.1%

How do you tell that you have the right version of CoB? It's the only one that doesn't visibly impact any of your stats. AC, THAC0, HP, saves - those can all be seen somewhere on your character sheet. The luck bonus we want, which comes up 10% of the time, is the only invisible one.

Grond0

jmerry wrote: »

No, we did (at least some of) the math earlier in the thread. They aren't equally likely outcomes.

If you have all the luck - meaning that you got the right version of Chaos of Battle, at cleric level 7 or higher - then it's absolutely guaranteed to give you the maximum 138 damage. Only a (critical) miss on the attack roll can stop you.

With +3 luck (no CoB), it's about 1/5 each to get 134 or 138 damage, and could theoretically go as low as 106. But that's down in the extremely unlikely tail. Your six observed outcomes cover about 98% of the possible outcomes. Probabilities, assuming a random version of CoB:

138: 27.8%
134: 17.8%
130: 24.4%
126: 14.1%
122: 10.1%
118: 3.6%
114: 1.5%
110: 0.3%
106: 0.1%

How do you tell that you have the right version of CoB? It's the only one that doesn't visibly impact any of your stats. AC, THAC0, HP, saves - those can all be seen somewhere on your character sheet. The luck bonus we want, which comes up 10% of the time, is the only invisible one.

I agree with the reasoning and the spread of possible results. However, the detailed %s look odd. I think the chance of getting 138 for instance is the chance of getting an adjusted result of 6 from each of 4 dice. The chance of that for each die is 2/3, so the overall chance is that to the power of 4 - or just under 20%. The chances given for other higher scores similarly look a little out.

jmerry

That's the effect of Chaos of Battle. 10% of the time, it gives you another +2 luck (+5 total) and all of the damage dice are adjusted to 6. The other 90% of the time, it's the table you're expecting. So ... scale all the percentages down by a tenth, and add 10% to the top entry.

Grond0

Right, sorry - I didn't read your earlier post carefully enough and assumed the CoB was not helping rather than helping some of the time.

sarevok57

i had the luck bonus from the chaos of battle, i was aware that if non of the stats changed i was getting the luck bonus, so i kept reloading until that happened

SirBatince

one real use for this scenario is one-shotting elminster for his sweet xp. can probably do it a few times aswell.

lroumen

Now I recommend an area change and test it on the real foe.